Biopharmaceutical manufacturing capacity, efficiency, flexibility and economics are all important outputs for organisations to optimize and continuously review. BioSolve Process is the biopharmaceutical industry’s most powerful software for bioprocess analysis. Due to the complexity of therapeutic manufacturing there are many variables contributing to the overall manufacturing performance. BioSolve Process has inbuilt tools to evaluate many input variables and to illustrate the results of the multi-variate decision space. However, we are always looking to improve the speed and ease with which decisions can be made and, in this instance, how quickly an optimum facility setup and operation can be determined for a given demand.
In collaboration with Innovate UK and the University of Manchester (UoM), Biopharm Services is involved in a Knowledge Transfer Partnership (KTP) project to investigate and implement the use of optimisation algorithms with BioSolve Process. This project is led by a KTP Associate, Folarin Oyebolu, whose prior research involved developing optimisation algorithms for biopharmaceutical manufacturing[1]. Specialist support from UoM includes Richard Allmendinger (Senior Lecturer in Data Science and Business Engagement Lead of Alliance Manchester Business School) and Jonathan Shapiro (Head of the Machine Learning and Optimisation Research Group in the School of Computer Science). Both Richard and Jonathan have expertise in the intersection of data science, machine learning, optimisation, and their applications to real-world problems.

Figure 1 Overview of optimisation tool framework, showing flows of information between the algorithm implemented in Python and the BioSolve Process software. After the user has defined the problem (i.e., selected decision variables, constraints, and objectives), the algorithm suggests decision variables to evaluate. These are then evaluated by BioSolve Process’ analysis model and the results are fed back to the algorithm. The algorithm will then select new decision variables to be evaluated in BioSolve Process based on those results. This loop continues until a specified number of loop iterations is completed.
For this project, the optimisation algorithm selected is Bayesian optimisation[2], which is used extensively to tune computationally expensive machine-learning models[3]. This is a technique that requires only a few evaluations to arrive at near optimal solutions. The goal of this work was to extend BioSolve Process with a Bayesian optimisation tool that automates the selection of the most efficient processes, within a few minutes. An overview of this framework is presented in Figure 1. This test case sought to optimize the production of 300kg/yr of monoclonal antibody. The algorithm was customised to deal with discrete and categorical variables (stainless or single-use, number of reactors, pooling strategy, etc.), constraints (such as shift pattern), and multiple conflicting objectives (COGS, CAPEX).
A single run of the optimization procedure is a continuous loop that takes a few minutes to terminate. Each iteration consists of an automated choice of a set of decision variables, followed by its evaluation (i.e., BioSolve analysis to calculate COGS and CAPEX). In this test case, the optimum decisions were achieved in 20-30 iterations of this loop (<20sec per iteration) which is about a tenth of the entire search space.
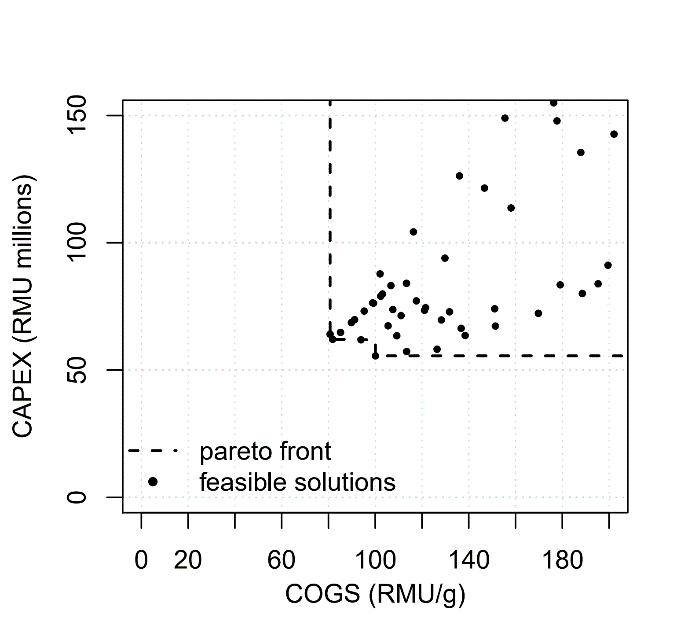
Figure 2 Pareto frontier for the multi-objective minimisation of COGS and CAPEX at 300kg/yr throughput. Other feasible but dominated points are shown in this plot.
Capital expenditure was plotted against COGS at the 300 kg/yr scale for each set of decision variables in Figure 2. This figure shows that the process with the lowest COGS does not have the lowest capital expenditure (and vice-versa). It also illustrates that although a general positive correlation exists between these objectives, a slight trade-off persists. Table 1 summarises the Pareto set of solutions. This is the set of solutions where, for each solution, none of the objectives can be improved in value without degrading some of the other objective values[4]. This preparation of the Pareto set is normally part of our consultancy services, and is an automated feature of the optimisation tool.
Table 1 Pareto set of process configurations (solutions) for the 300kg/yr case, showing the COGS and CAPEX objective values. COGS in RMU/g, and CAPEX in RMU millions.
| Process | Installed Reactors | Pooled Reactors | COGS | CAPEX |
| SS | 1 | 1 | 80.7 | 64 |
| SU | 3 | 3 | 81.8 | 62 |
| SU | 3 | 1 | 100 | 56 |
As can be seen in Figure 2, the objective space ranges from 56M RMU up to at least 150M RMU for capital expenditure and from 80 RMU/g to at least 200 RMU/g. This means that significant savings could be determined quickly using this integration of BioSolve Process and the Bayesian optimization tool especially on large and complex problems.
Please let us know if you are interested in this work. A poster was presented at the 16th Annual bioProcessUK Conference (Liverpool, 2019) and is available here.
We intend to expand the case study to include continuous operations, downstream operations, and the manufacture of alternative biopharmaceuticals (viruses, plasmid, CAR-T).
[1] Oyebolu, F. B., van Lidth de Jeude, J., Siganporia, C. C., Farid, S. S., Allmendinger, R., & Branke, J. (2017). A new lot sizing and scheduling heuristic for multi-site biopharmaceutical production. Journal of Heuristics, 23(4), 231–256. https://doi.org/10.1007/s10732-017-9338-9
[2] Knowles, J. (2006). ParEGO: a hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems. IEEE Transactions on Evolutionary Computation, 10(1), 50–66. https://doi.org/10.1109/TEVC.2005.851274
[3] Snoek, J., Larochelle, H., & Adams, R. P. (2012). Practical Bayesian optimization of machine learning algorithms. Advances in Neural Information Processing Systems, 4, 2951–2959. Retrieved from https://arxiv.org/pdf/1206.2944.pdf
[4] “Pareto Front”. Retrieved 18 Mar. 20 from: http://www.cenaero.be/Page.asp?docid=27103&



